
Elk Grove Legal Trouble: California AG Sends Stern Warning!
Yearning for insights into California's governance dynamics? Discover the implications of the Attorney General's actions on Elk Grove's affordable housing stance.

Yearning for insights into California's governance dynamics? Discover the implications of the Attorney General's actions on Elk Grove's affordable housing stance.

On an epic journey from California to Michigan, a dog's resilience and determination lead to a heartwarming reunion – but what obstacles did Mishka face along the way?

Faced with unprecedented layoffs and project halts, Apple's future hangs in the balance, sparking intense speculation and curiosity.

Jump into the details of California's Shift-to-Office plan affecting state teleworkers, promising insights on who's in, who's out, and how it impacts them!
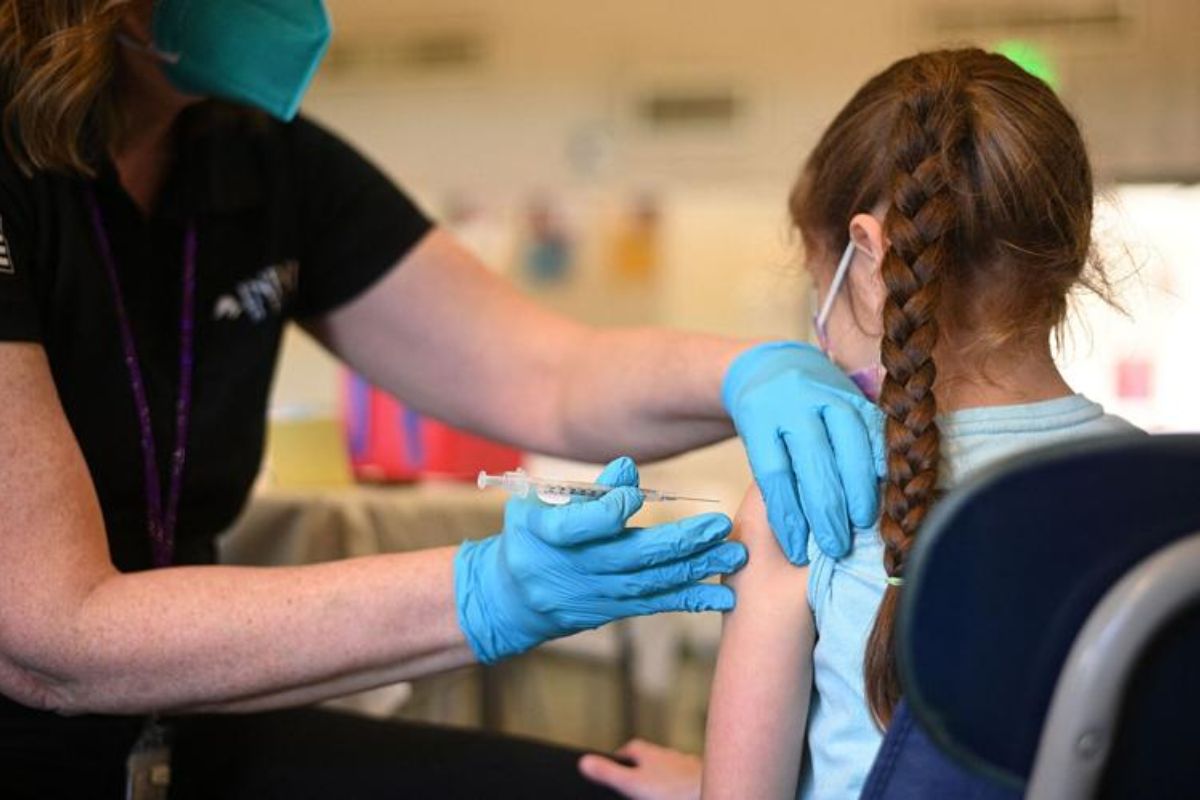
Keen to learn how a California doctor's innovative method is revolutionizing needle pain for kids? Keep reading to discover this genius solution!

Faced with a dramatic landslide, California's Highway 1 crumbles, leading to a heroic rescue operation that saves hundreds – find out how!

A groundbreaking proposal in California hints at a significant electricity rate reduction, sparking excitement and speculation about potential impacts on consumers and energy distribution.

Bold plan to enhance safety with 500 cameras in Oakland sparks debate on privacy and effectiveness – find out more about this controversial initiative.

Prepare for a gripping account of a fatal avalanche at Palisades Tahoe ski resort, leaving readers on edge with unfolding details.

Yearning for adventure, the Jacobs family embarks on an epic journey from California to Bentonville, their transformative experiences leaving a lasting impact – ready to discover more?